Tính đường phân giác biết số đo ba cạnh (Lớp 8)

Bài toán: Cho tam giác ABC có phân giác AD. Tính AD.

Hoặc: Cho tam giác ABC có phân giác AD. Chứng minh : AD^2 = AB.AC − BD.DC

Giải:
Hình vẽ: Vẽ tam giác ABC có AD là tia phân giác, vẽ góc BCx = 1/2 góc BAC (Tia Cx nằm dưới BC). Cx cắt AD ở E.

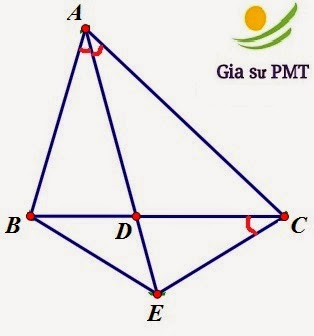
Ta có tam giác ABD đồng dạng với tam giác AEC (g-g)
Suy ra AD/AC = AB/AE
⇒AB.AC = AD.AE = AD.(AD + DE) = AD^2 + AD.DE (1)
Ta có tam giác ABD đồng dạng với tam giác CED (g-g)
Suy ra AD/CD = DB/DE
⇒AD.DE = DB.DC (2)
Từ (1) và (2) suy ra: AD^2 = AB.AC − DB.DC